Your feedback can help us improve and enhance our services to the public. Tell us what matters to you in our online Customer Satisfaction Survey.
The lowest level of the WPI calculation uses the Jevons index formula. This is a change introduced for Base Year 2021 = 100. The lowest level calculates the index for all prices of the same product group for one respondent. The 2015 series used the weighted Laspeyres index formula, where the weights were the revenue shares for individual products estimated by the respondent. The Jevons formula treats all the products for a respondent within a product group equally.
A weighted Laspeyres formula requires consistently high-quality information from each respondent for the relative split of their products. As these can evolve over time, the information provided to the CSO could be misleading. The Jevons formula avoids this burden on respondents.
The Jevons index is defined as:
The value pit refers to the price of product i at time t, while and pi0 is the price of product i in the price reference period. In the 2021 as 100 series, the price reference period is December 2020. n is the number of products the respondent supplied prices for within the product group. In practice the chained version of the Jevons formula is used. This is explained in the next section.
The WPI indices at all higher levels of aggregation are compiled using a variant of the fixed weighted Laspeyres index formula. The Laspeyres index for these higher levels of aggregation is defined as:
The value Iit refers to the price index of aggregate i at time t, while Ii0 is the price index of aggregate i in the price reference period. In the 2021 as 100 series, the price reference period is December 2020. The weights wi0 are the revenue shares for individual aggregates in the weight reference period. While the objective is the calculation of a Laspeyres index, where the price and weight reference periods are the same, in practice the index takes the form of a Young index (see below). In a Young index, the weight reference period may be different from the price reference period due to time lags in data availability.
Note that indices included in the WPI release are expressed in the standard form where a value of 100 means that there is no change in the index between the current and base periods.
Also, in practice the chained version of the Laspeyres formula is used. This is explained in the next section.
The Jevons and Laspeyres formulae above are direct indices i.e. they compare prices or indices in the current period to those in the reference period. Direct index calculations require the same sample to be used during the current and reference period. In practice, products and respondents are dropped from the index over time and new products and respondents introduced. Using a direct index reduces the data available for the index to the subsample which is present in both the current and reference time periods.
An alternative to a direct index is a chain index. In a chain index, each link in the chain is calculated by comparing the prices in the current period to those in the previous period. While sample changes over the full length of the series can be large, only a small number of products or respondents will change between two subsequent time periods. Using a chain index minimises the reduction in usable data due to sample changes.
The chained version of the Jevons index is:
And then
The direct and chained version of the Jevons formula give the same answer if the respondent supplies prices for the same products within a product group from the reference period to the current period.
For the Laspeyres index the chain links are chained together to obtain a long-term index by updating the quantities used to weight the price relatives each month as shown below. In the first month, the chain index calculation is the same as the direct index:
For each unit i, the calculation 
gives an “updated value” for i, i.e. its weight in the reference period updated by the relative 
or the price change between period 1 and period 0. Denoting these updated values as wi1, the index for the second month is calculated as:
Again, the updated values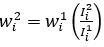 
are used to weight the relatives in the subsequent month:
And in general, the index at time t is given by:
Where the sample remains the same, the chain index equals the direct index. For example, at time t=3:
To compile the WPI indices, first the price indices of the lowest level elementary aggregates are calculated. Then weighted averages of these elementary price indices are used to obtain higher-level indices. The calculations are done in several stages reflecting the hierarchical structure of the WPI.
In practice the method of compilation of the indices means that base period commodity values are progressively updated each month and the price indices are derived by dividing the aggregate current monthly value by the corresponding base period value.
(i) Each elementary aggregate is a product group for a single respondent. Elementary price indices are calculated for these elementary aggregates. The elementary price index is a chained month-to-month Jevons index as described above. Only products which have prices in both the current and previous month are included in the calculation.
(ii) The elementary aggregates are used to calculate price indices at the product group level. A weighted average of the price indices of different respondents within each product group is calculated where the weights are the share of sales recorded by each respondent in that product group. These weights are estimated from responses to CSO surveys. This weighted average calculation is a Young index. The general formula for a Young index is:
Here, PY0:t is the product group index for time t, the sum Σ is over all respondents within a product group, Ii0:t is the elementary price index for respondent i in the product group, and wib is the weight of the respondent in the product group in period b, which typically precedes the reference period 0. In the WPI, a chained Young index is used instead of a direct index, for the same reasons as described above for the Laspeyres index. The chained version of the Young index, which is equivalent to the direct Young index where the sample remains the same, is given by:
Ii0:t-1 is the elementary price index for respondent i in the product group in the previous period, while Iit-1:t is the month-on-month index comparing the current to the previous period. This month-on-month index is the ratio of the indices for period t and t - 1.
(iii) A weighted average of month-on-month product group price indices within a NACE group (3-digit NACE) is used to calculate NACE group price indices. The calculation is a chained Young index as detailed in the previous step, where the indices Iit-1:t are the month-on-month product group price indices. The weights wib are the relative proportions of each product group within the corresponding NACE group.
(iv) A weighted average of month-on-month NACE group price indices within a NACE division (2-digit NACE) is used to calculate NACE division price indices. The calculation is a chained Young index as detailed previously, where the indices Iit-1:t are the month-on-month NACE group price indices. The weights used are the relative proportions of each NACE group within the corresponding NACE division.
(v) Other higher-level aggregates are calculated as weighted averages of NACE group price indices using the same method. Again, the calculation is a chained Young index, where the indices Iit-1:t are the month-on-month NACE group price indices. The weights used are sums of the corresponding weights from the lower levels of aggregation.
(vi) Certain indices are calculated on a net sector basis. This means that sales from one industry in a sector to another industry in the same sector are excluded from the weighting calculations. This is to prevent double counting of price changes as products flow through different production processes.
(vii) To get the final Base Year Indices at NACE group, NACE division and other levels of aggregation, the base period indices are rescaled by dividing by the mean of the corresponding 12 monthly indices during 2021.
The WPI compilation process is illustrated by the chart in Appendix 1.